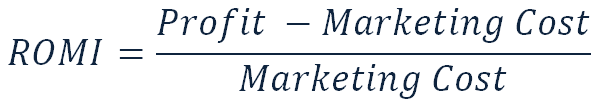Konstantin Sakhnov, the research advisor of ‘Online Gaming Project Management’ education initiative and the Head of Game design at Rocket Jump, told us how to calculate the return on investments in gaming projects and shared with us some specific methods for doing it.

Image Credit: App2Top.ru
How can you verify the ROI?
There are various strategies for gaining returns on gaming products. Some make money on ads, others on copies or subscriptions. You can funnel traffic through a cross-promo or pray for virality. However, for F2P games the most simplified ROI model looks as follows:
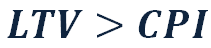
Here LTV (Lifetime Value) – average cash generated from a single user over the lifetime of playing the game. And CPI (Cost Per Install) – is the cost of acquisition of one player. And if CPI can be learned from partners who advertise us, and we can take efforts to reduce it through optimizing our promo channel spendings among other things, LTV primarily relies on our product.
LTV calculation methods
1. Using audience size and revenue
If a game is already in circulation, we can find out how much it grossed over a certain period of time. We also know how many players visited the project during the same period. By dividing the revenue for the period by the number of players visiting the game during the same time we get the required index.

This type of estimation has two drawbacks. First, it works only with currently running projects, so we have no possibility for prediction. Second, in reality, we always have a difficulty defining the timeframe for data collection.
2. Using average Lifetime (LT)
ARPDAU – shows the average amount of revenue from one player. In fact, it is ARPU divided by 30.
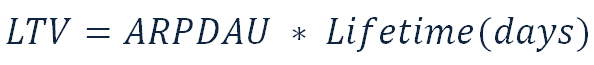
Lifetime (days) – shows the number of days a player “lives” in the game.
While predicting our ROI, we looked at ARPU of other projects of our genre and approximated the ARPU of our game. Then we need to calculate the Lifetime. It can be done knowing the retention of your project. There is a whole range of methods available for calculating the retention:
- Classic retention – percentage of players who started playing for the first time seven days ago and returned at the settlement date.
- Rolling retention – players who returned on the settlement date and later.
- Return retention – players who returned at least once from the 1st to the settlement date.
- Full retention – players returning every day until the settlement date inclusive.
- Bracket-dependent return retention – returning during defined timeframes.
However, at the stage of prediction, we still do not have enough statistics, and therefore, we can only estimate the retention of our game or calculate its minimal value required for the project’s breakeven.
The retention of each next day cannot be higher than that for the previous day. The chart of this function looks as follows:
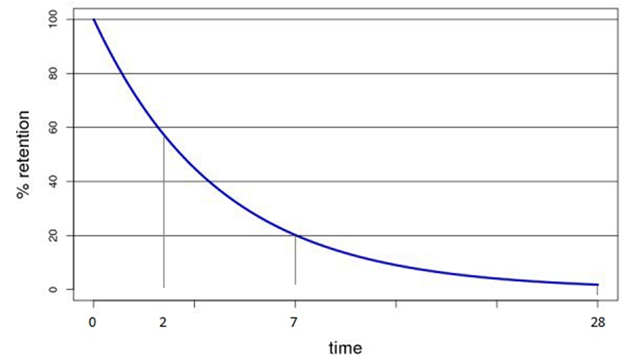
Using 3 control points, for instance: retention on the 1st, 7th, and 28th days we are able to approximate this function using a hyperbola:
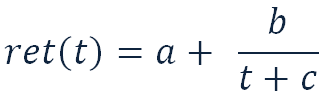
Here we place the days’ number for t (1, 7, 28 or others) and replace ret(t) with the project’s retention for this day. You can get these figures by comparing your game with titles of a similar genre (except Top Grossing).
Then, we write the system of three such equations, substituting into it the corresponding values of t and ret(t). Solving the system of three simple equations with three unknowns, we find the coefficients a, b, and c.
Now we have an approximated formula of retention function. The area under this curve is the desired value of our Lifetime. Turning to the school course of integration, we can remember that the area underneath the curve is calculated through a definite integral:
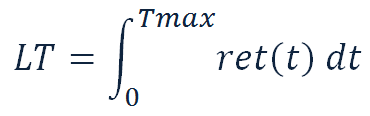
We substitute the obtained coefficients and integrate. After calculations we get:
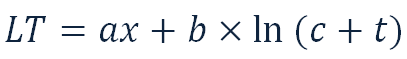
With substitutions from 0 to Tmax (28 days). It is worth mentioning that the obtained result has at least two inaccuracies:
- Approximation error
- Incomplete interval
If the first point is clear, the second requires some commenting. We calculated the integral from 0 to 28 days. This assumes that all of the players spend no more than 28 days in the game. But this is not the case. There is always a core community of players with a high rate of retention, who play for a few months, and retention does not converge to 0 on the 30th day. To take this nuance into account, we add the second month to the curve, making an assumption that by the 60th day at least half of those who have reached the 28th day would stay playing. Such amendment would allow for a more accurate value of Lifetime.
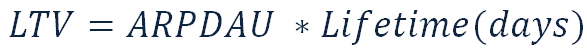
We calculated the Lifetime and now we substitute it into the original LTV calculation formula and obtain the required value:

In some cases, when a project’s retention is rather high, we need to consider that the money invested into the project today will have a different value tomorrow. For this we need to apply a discount rate WACC (Weighted Average Cost of Capital) to our calculations.